Reinforcemant Learning (15)

Recall the Bellman Equation:

$$\begin{aligned} \left(T^\pi f\right)(s, a) & =R(s, a)+\gamma \mathbb{E}_{s^{\prime}\sim P(k, a)}\left[f\left(s^{\prime}, \pi\right)\right] \\ & =\mathbb{E}\left[r+\gamma \cdot f\left(s^{\prime}, \pi\right) \mid s, a\right] . \end{aligned}$$

with empirically equals to:

$$\frac{1}{n} \sum_{i=1}^n\left(r_i+\gamma \theta_{k_1}\left(s_i^{\prime}, \pi\right)\right) .$$

with tuples $(s_t, a_t, r_t, s_{t+1})$ in the long trajectory, applying the running average:

$$Q_k(s_t, a_t) \leftarrow Q_k(s_t, a_t)+\alpha(r_t+\gamma Q_{k-1}(s_{t+1}, \pi)-Q_k(s_t, a_t))$$

SARSA

$$Q\left(s_{t}, a_{t}\right) \leftarrow Q\left(s_{t}, a_{t}\right)+\alpha\left(r_{t}+\gamma Q\left(s_{t}+1, a_{t}+1\right)-Q\left(s_{t}, a_{t}\right)\right)$$

Notice that SARSA is not applicable for deterministic policy, because it requires a non-zero probability distribution over all st0ate-action pairs ( $\forall (s,a) \in S\times A$ ), but the only possible action for a certain state is determined by the policy.

SARSA with $\epsilon$ -greedy policy

How are the $s, a$ data pairs picked in SARSA?

At each time step t, with probability $\epsilon$ , choose a from the action space uniformly at random. otherwise, $a_t = \argmax_a Q(s_t, a)$

When sampling s-a-r-s-a tuple along the trajectory, the first action in the tuple is actually generated with last version of $Q$ , so we can say SARSA is not 100% “on policy”.
{: .prompt-info }

Does SARSA converge to optimal policy?

The cliff example (pg 132 of Sutton & Barto)

• Deterministic navigation, high penalty when falling off the clif
• Optimal policy: walk near the cliff
• Unless epsilon is super small, SARSA will avoid the cliff

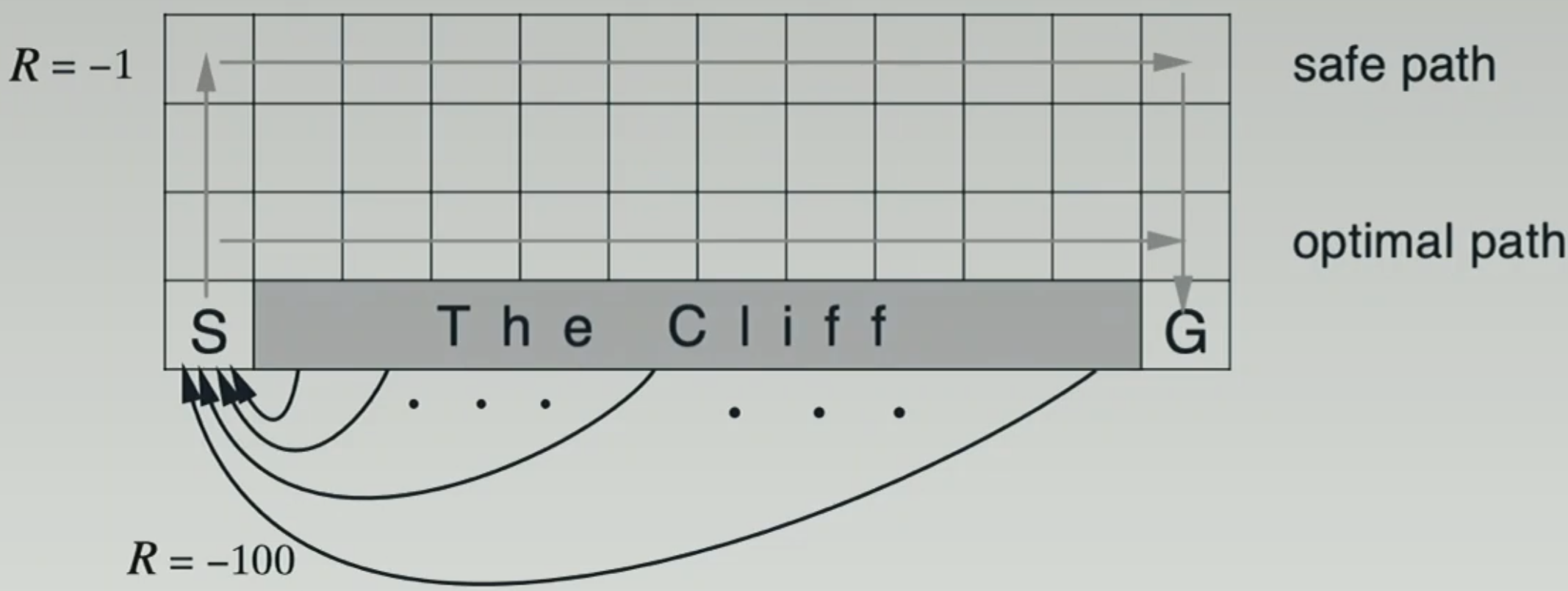
cliff example

The optimal path is along the side of the cliff, but on this path, the $\epsilon$ -greedy SARSA will often see large penalty (falling off the cliff) and therefore, choose the safe path instead.

softmax

$\epsilon$-greedy can be replaged by softmax: chooses action a with probability

$$\frac{\exp(Q(s,a) / T)}{\sum_{a'} \exp(Q(s,a') / T)}$$

where $T$ is temperature.