Distributed System (9)

Mutual Exclusion

Ricart-Agrawala’s Algorithm

• enter() at process Pi
  • set state to Wanted
  • multicast “Request” $<T_i, P_i>$ to all processes
    where $T_i =$ current Lamport timestamp at $P_i$
  • wait until all processes send back “Reply”
  • change state to Held and enter the CS
• On receipt of a Request $<T_j, P_j>$ at $P_i$ ( $i \ne j$ ):
  • if (state = Held) or (state = Wanted and $(T_i, i) < (T_j, j)$ ) *// lexicographic ordering in $(T_j, P_j)$ *
    • add request to local queue (of waiting requests)
  • else send “Reply” to $P_j$
• exit() at process Pi
  • change state to Released and “Reply” to all queued requests.

Maekawa’s Algorithm

put $N$ processes in a $\sqrt{N}$ by $\sqrt{N}$ matrix and for each $P_i$ , its voting set $V_i =$ row containing $P_i$ + column containing $P_i$ (each set size = $2\sqrt{N}-1$ )

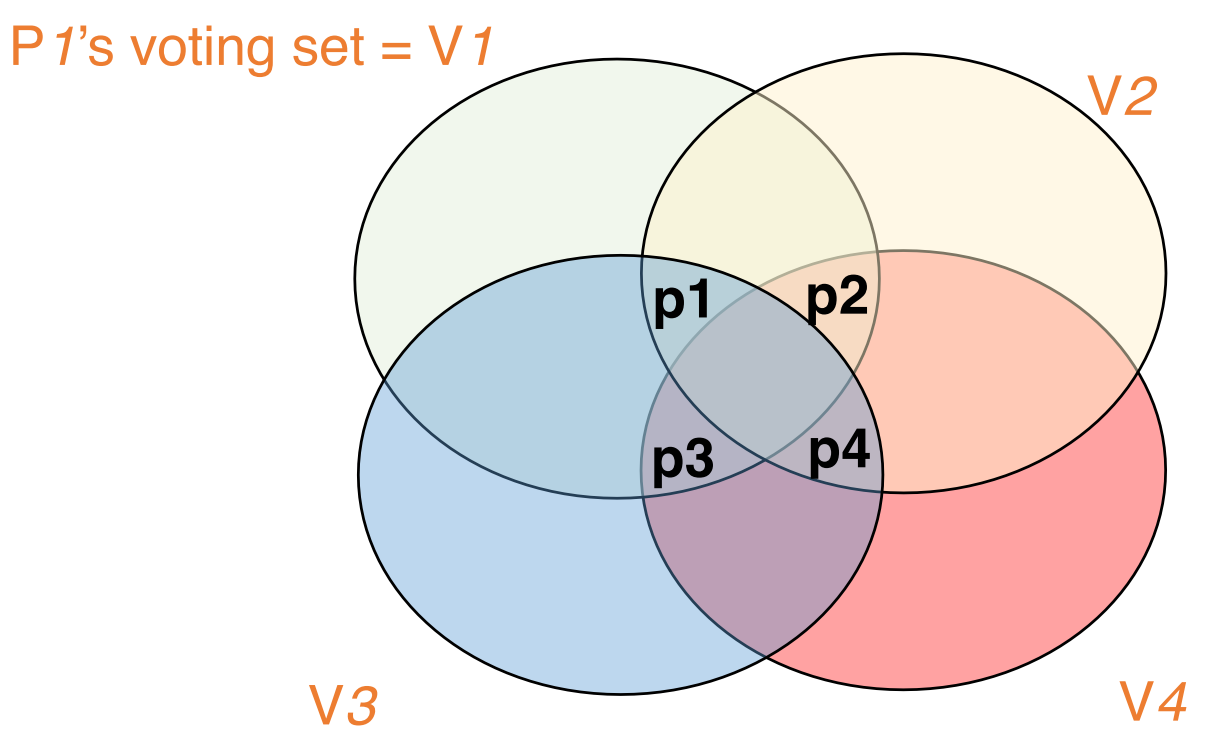
voting set

• state = Released, voted = false
• enter() at process Pi:
  • state = Wanted
  • Multicast Request message to all processes in $V_i$
  • Wait for Reply (vote) messages from all processes in $V_i$ (including vote from self)
  • state = Held
• exit() at process Pi:
  • state = Released
  • Multicast Release to all processes in $V_i$ :
• When $P_i$ receives a Request from $P_j$ :
  • if (state $==$ Held OR voted $==$ true)
    • queue Request
  • else
    • send Reply to $P_j$ and set voted $=$ true
• When $P_i$ receives a Release from $P_j$ :
  • if (queue empty)
    • voted $=$ false
  • else
    • dequeue head of queue as $P_k$
    • Send Reply only to $P_k$
    • voted = true