Perceptron
Recall the sigmiod loss.
Define the perceptron hinge loss:
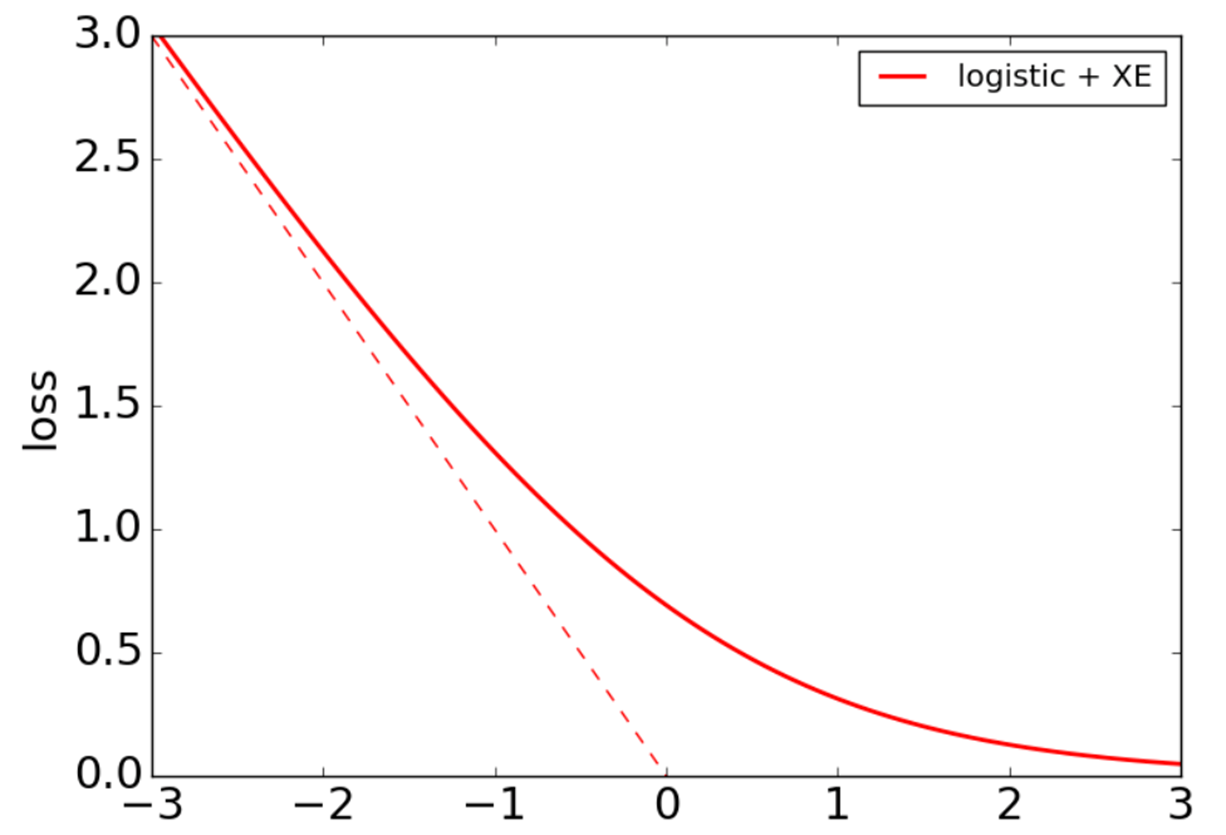
l(w,xi,yi)=max(0,−yiwTxi)
Training process: find w that minimizes (with SGD)
L(w)=n1i=1∑nl(w,xi,yi)=n1i=1∑nmax(0,−yiwTxi)
The graident of perceptron loss is:
∇l(w,xi,yi)=−I[yiwTxi<0]yixi
Support vector machine (SVM)
maximize the distance between the hyperplane
and the closest training example, where the distance is given by ∥w∥∣wTx0∣ .

finding hyperplane
Assuming the data is linearly separable, we can fix the scale of w so that yiwTxi=1 for support vectors and yiwTxi≥1 for all other points.
i.e. We want to maximize margin ∥w∥1 while correctly classifying all training data: yiwTxi≥1 , or
wmin21∥w∥2 s.t. yiwTxi≥1∀i.
Soft margin
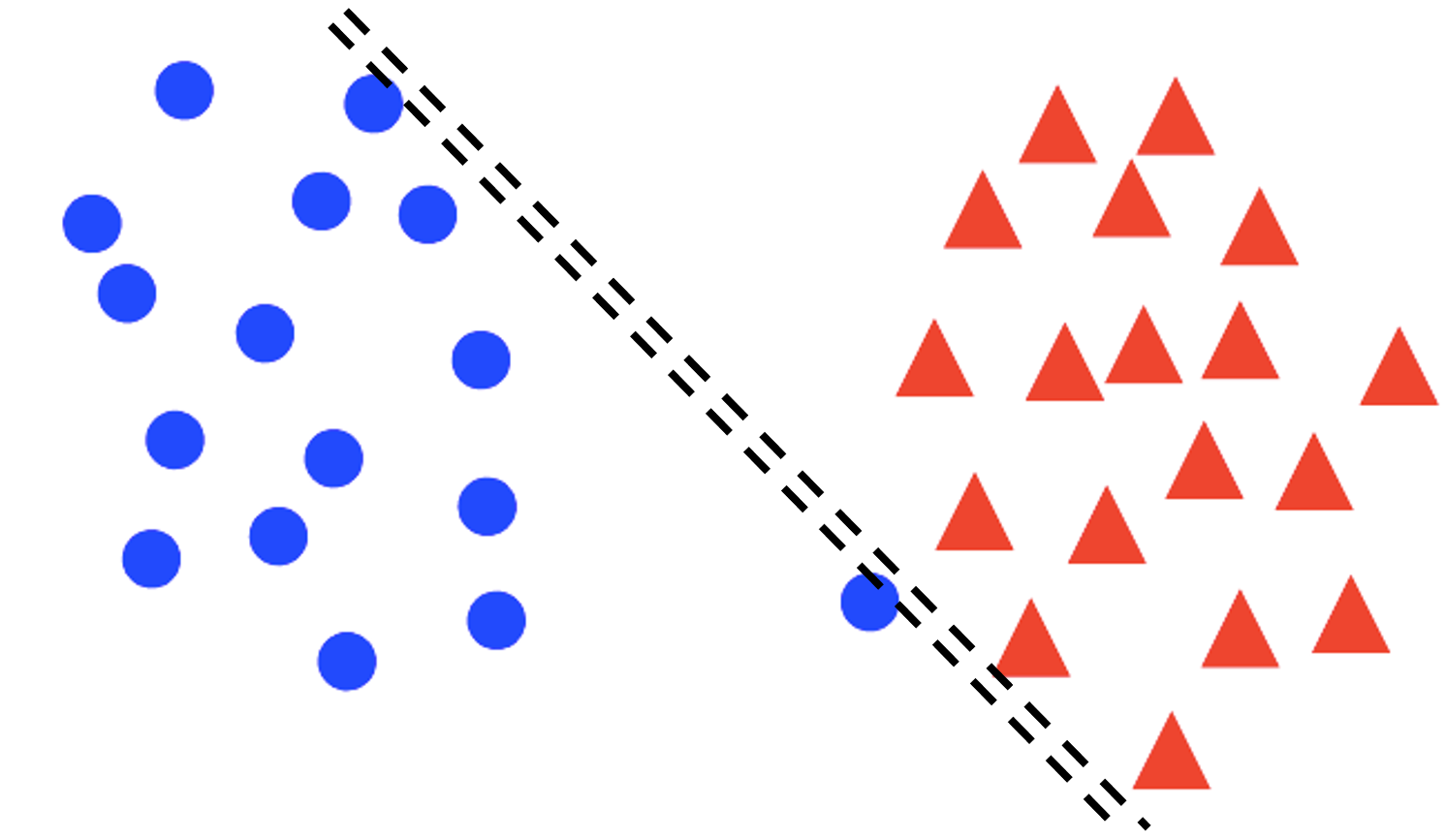
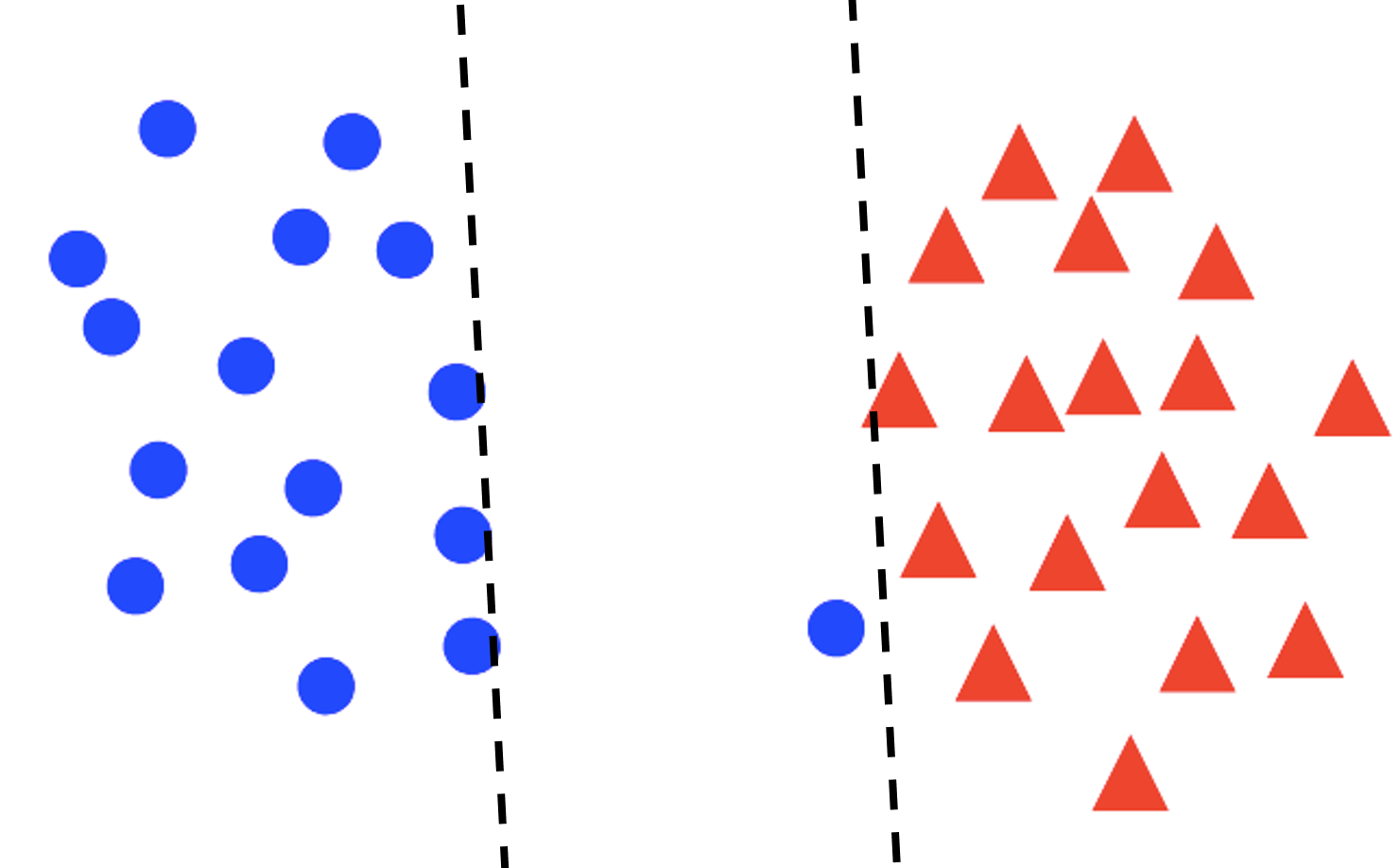
For non-separable and some separable data, we may prefer a larger margin with a few constraints violated.
wmin Maximize margin − (regularization) 2λ∥w∥2+Minimize misclassification loss i=1∑nmax[0,1−yiwTxi]
The loss is similar to the perceptron loss.
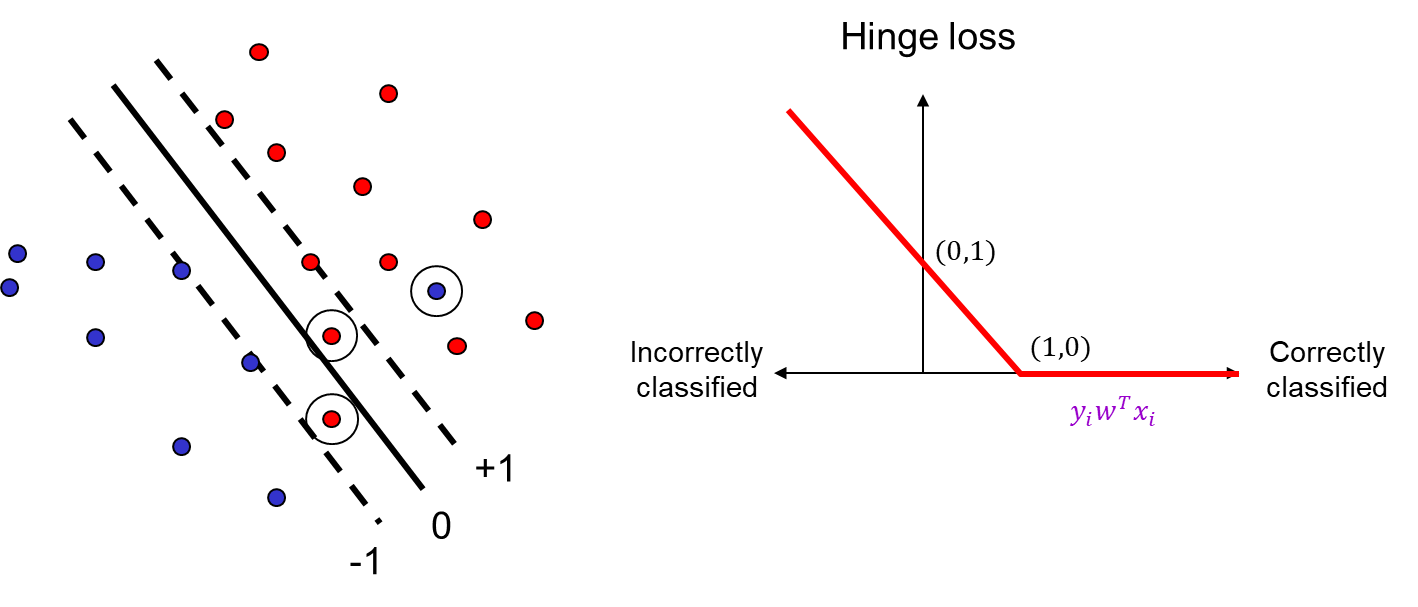
SVM and Hinge loss
This loss function tolerates wrongly classified points to get a larger margin.
SGD update
The loss function is l(w,xi,yi)=2nλ∥w∥2+max[0,1−yiwTxi] and its gradient is
∇l(w,xi,yi)=nλw−I[yiwTxi<1]yixi.
General recipe
empirical loss = empirical loss + data loss
L^(w)=λR(w)+n1i=1∑nl(w,xi,yi)
regularization
- L2 regularization: R(w)=21∥w∥22
- L1 regularization: R(w)=21∥w∥1:=∑dw(d)
The gradient of loss function with L1 regularization is
∇L^(w)=λsgn(w)+i=1∑n∇l(w,xi,yi)
L1 regularization encourages sparsity weight.
Multi-class classification
Multi-class perceptron
Learn C scoring functions: f1,f2,…,fC
and y^=argmaxcfc(x)
Multi-class perceptrons:
fc(x)=wcTx
use sum of hinge losses:
l(W,xi,yi)=c=yi∑max[0,wcTxi−wyiTxi]
Update rule: for each c s.t. wcTxi>wyiTxi :
wyiwc←wyi+ηxi←wc−ηxi
Multi-class SVM
l(W,xi,yi)=2nλ∥W∥2+c=yi∑max[0,1−wyiTxi+wcTxi]
Softmax
Softmax maps a vector into probability.
softmax(f1,…,fc)=(∑jexp(fj)exp(f1),…,∑jexp(fj)exp(fC))
Compared to sigmoid: for 2 class cases,
softmax(f,−f)=(σ(2f),σ(−2f))
loss function
The negative log likelihood loss
l(W,xi,yi)=−logPW(yi∣xi)=−log(∑jexp(wjTxi)exp(wyiTxi))
This is also the cross-entropy between the empirical distribution P^ and estimated distribution PW :
−C∑P^(c∣xi)logPW(c∣xi)
More on Softmax
Avoid overflow
∑jexp(fj)exp(fc)=∑jKexp(fj)Kexp(fc)=∑jexp(fj+logK)exp(fc+logK)
and let
logK:=−jmaxfj
Temperature
softmax(f1,…,fc;T)=(∑jexp(fj/T)exp(f1/T),…,∑jexp(fj/T)exp(fC/T))
High temperature: close to uniform distribution.
Label smoothing
Use “Soft” prediction targets. i.e. Use empirical distribution
P^(c∣xi)={1−ϵC−1ϵc=yic=yi.
Label smoothing is a form of regularization to avoid overly confident predictions, account for label noise





