Reinforcement Learning (2-4)

Markov Decision Processes

Infinite-horizon discounted MDPs

An MDP $M = (S, A, P, R, \gamma)$ consists of:

• State space $S$ .
• Action space $A$ .
• Transition function $P$ : $S \times A \rightarrow \Delta(S)$ . $\Delta(S)$ is the probability simplex over $S$ , i.e., all non-negative vectors of length $| S|$ that sums up to $1$ .
• Reward function $R$ : $S \times A \rightarrow \mathbb{R}$ . (deterministic reward function)
• Discount factor $\gamma \in [0,1]$

The agent

1. starts in some state $s_1$
2. takes action $a_1$
3. receives reward $r_1 = R(s_1, a_1)$
4. transitions to $s_2 \sim P(s_1, a_1)$
5. takes action $a_2$
6. … and so on so forth — the process continues forever.

Objective: (discounted) expected total reward

• Other terms used: return, value, utility, long-term reward, etc

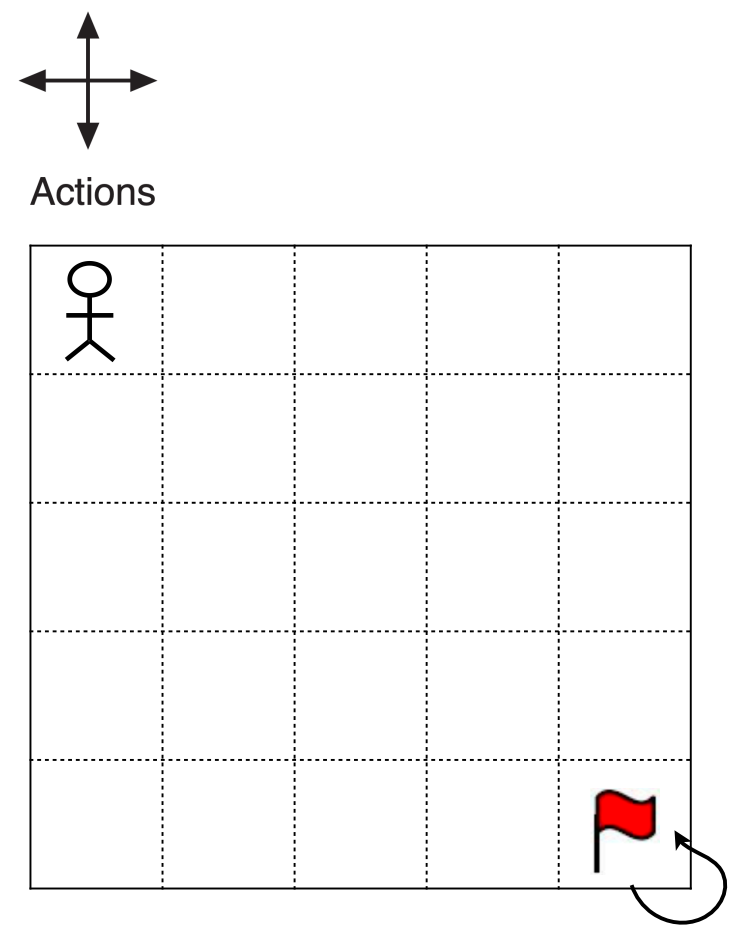
Example: Gridworld

• State: grid x, y
• Action: N, S, E, W
• Dynamics:
  • most cases: move to adjacent grid
  • meet wall or reached goal: keep in the current state
• Reward:
  • $0$ in the goal state
  • $-1$ everywhere else
• Discount factor $\gamma$ : 0.99

discounting

$\gamma = 1 $allows some strategies to obtain$ -\infty$ expected return.

For $\gamma < 1$ , the total reward is finite.

finite horizon vs. infinite-horizon discounted MDP

• For finite-horizon (finite acitons), $\gamma$ can be $1$ .
• For infinite-horizon (infinite acitons), $\gamma < 1$ .

Value and policy

Take action that maximize

$$\mathbb{E}\left[\sum_{t=1}^{\infty} \gamma^{t-1} r_t\right]$$

assume $r_t \in [0, R_{\max}]$ ,

$$\mathbb{E}\left[\sum_{t=1}^{\infty} \gamma^{t-1} r_t\right] \in \left[0,\frac{R_{\max}}{1-\gamma} \right].$$

A policy describes how the agent acts at a state:

$$a_t = \pi(s_t)$$

define value funtion

$$V^\pi (s) = \mathbb{E}\left[\sum_{t=1}^{\infty} \gamma^{t-1} r_t \middle| s_1 = s, \pi \right]$$

Bellman Equation

$$\begin{aligned} V^\pi(s) & =\mathbb{E}\left[\sum_{t=1}^{\infty} \gamma^{t-1} r_t \middle| s_1=s, \pi\right] \\ & =R(s, \pi(s))+\gamma\left\langle P(\cdot \middle| s, \pi(s)), V^\pi(\cdot)\right\rangle \end{aligned}$$

Detailed steps

$$\begin{aligned} V^\pi(s) & =\mathbb{E}\left[\sum_{t=1}^{\infty} \gamma^{t-1} r_t \middle| s_1=s, \pi\right] \\ & =\mathbb{E}\left[r_1+\sum_{t=2}^{\infty} \gamma^{t-1} r_t \middle| s_1=s, \pi\right] \\ & =R(s, \pi(s))+\sum_{s^{\prime} \in \mathcal{S}} P\left(s^{\prime} \middle| s, \pi(s)\right) \mathbb{E}\left[\gamma \sum_{t=2}^{\infty} \gamma^{t-2} r_t \middle| s_1=s, s_2=s^{\prime}, \pi\right] \\ & =R(s, \pi(s))+\sum_{s^{\prime} \in \mathcal{S}} P\left(s^{\prime} \middle| s, \pi(s)\right) \mathbb{E}\left[\gamma \sum_{t=2}^{\infty} \gamma^{t-2} r_t \middle| s_2=s^{\prime}, \pi\right] \\ & =R(s, \pi(s))+\gamma \sum_{s^{\prime} \in \mathcal{S}} P\left(s^{\prime} \middle| s, \pi(s)\right) \mathbb{E}\left[\sum_{t=1}^{\infty} \gamma^{t-1} r_t \middle| s_1=s^{\prime}, \pi\right] \\ & =R(s, \pi(s))+\gamma \sum_{s^{\prime} \in \mathcal{S}} P\left(s^{\prime} \middle| s, \pi(s)\right) V^\pi\left(s^{\prime}\right) \\ & =R(s, \pi(s))+\gamma\left\langle P(\cdot \middle| s, \pi(s)), V^\pi(\cdot)\right\rangle \end{aligned}$$

where $\langle\cdot, \cdot\rangle$ is Dot Product.

Matrix form

• $V^\pi$ as the $| S| \times 1$ vector $[V^\pi(s)]_{s \in S}$
• $R^\pi$ as the vector $[R(s, \pi(s))]_{s \in S}$
• $P^\pi$ as the matrix $[P(s' | s, \pi(s))]_{s \in S, s' \in S}$

$$\begin{gathered} V^\pi = R^\pi + \gamma P^\pi V^\pi \\ (I - \gamma P^\pi)V^\pi = R^\pi \\ V^\pi = (I - \gamma P^\pi)^{-1}R^\pi \\ \end{gathered}$$

Claim: $(I - \gamma P)$ is invertible.

Proof. It suffies to prove

$$\forall x \ne \vec{0} \in \mathbb{R}^S, \; (I - \gamma P^\pi)x \ne \vec{0}$$

then

$$\begin{aligned} &\| (I - \gamma P^\pi) x \| _{\infty} \\ =&\| x - \gamma P^\pi x \| _{\infty} \\ \ge&\| x\| _{\infty} - \gamma\| P^\pi x \| _{\infty} \\ \ge&\| x\| _{\infty} - \gamma\| x\| _{\infty} \\ =&(1 - \gamma)\| x\| _{\infty} \\ \ge&\| x\| _{\infty} \\ >& 0 \blacksquare \end{aligned}$$

Generalize to stochastic policies

$$V^\pi(s) = \mathbb{E}_{a \sim \pi(\cdot \mid s), s^{\prime} \sim P(\cdot \mid s, a)}\left[R(s, a)+\gamma V^\pi\left(s^{\prime}\right)\right]$$

Matrix form

$$V^\pi = R^\pi + \gamma P^\pi V^\pi$$

still holds for

$$\begin{aligned} & R^\pi(s)=\mathbb{E}_{a \sim \pi(\cdot \mid s)}[R(s, a)] \\ & P^\pi\left(s^{\prime} \mid s\right)=\sum_{a \in \mathcal{A}} \pi(a \mid s) P\left(s^{\prime} \mid s, a\right) \end{aligned}$$

Optimality

For infinite-horizon discounted MDPs, there always exists a stationary and deterministic policy that is optimal for all starting states simultaneously.

Optimal policy $\pi^\star$ and

$$V^\star := V^{\pi^\star }$$

Bellman Optimality Equation

$$V^{*}(s)=\max_{a\in A}\left(R(s,a)+\gamma\mathbb{E}_{s^{\prime}\thicksim P(s,a)}\left[V^{*}(s^{\prime})\right]\right)$$

Q-functions

$$\begin{gathered} Q^{\pi}(s,a):=\mathbb{E}\left[\sum_{t=1}^{\infty}\gamma^{t-1}r_{t} \middle| s_1=s, a_1=a; \pi \right] \\ Q^\star := Q^{\pi^\star } \; \text{or} \\ V^{\pi}(s)=Q^{\pi}(s,\pi(s)) \;\; \text{or} \;\; Q^{\pi}(s,\pi)\\ \end{gathered}$$

Bellman equation for $Q$

$$\begin{gathered} Q^{\pi}(s,a)=R(s,a)+\gamma\mathbb{E}_{s^{\prime}\sim P(\cdot|s,a)}\left[Q^{\pi}(s^{\prime},\pi)\right] \\ Q^\star (s,a)=R(s,a)+\gamma\mathbb{E}_{s^{\prime}\sim P(\cdot|s,a)}\left[\max_{a^{\prime}\in A}Q^\star (s^{\prime},a^{\prime})\right] \end{gathered}$$

Define optimal $V$ and $\pi$ by $Q$

$$V^{*}(s)=\max_{a\in A}Q^{*}(s,a)=Q^{*}(s,\pi^{*}(s))$$

$$\pi^\star (s) = \argmax_{a \in A} Q^\star (s, a)$$

Fixed-horizon MDPs

Specified by $(S, A, R, P, H)$ , All trajectories end in precisely $H$ steps

$$\begin{gathered} V_{H+1}^\pi \equiv 0 \\ V_{h}^{\pi}(s)=R(s,\pi(s))+\mathbb{E}_{s'\sim P(s,a)}[V_{h+1}^{\pi}(s')] \end{gathered}$$