Reinforcement Learning (1)

example: Shortest Path

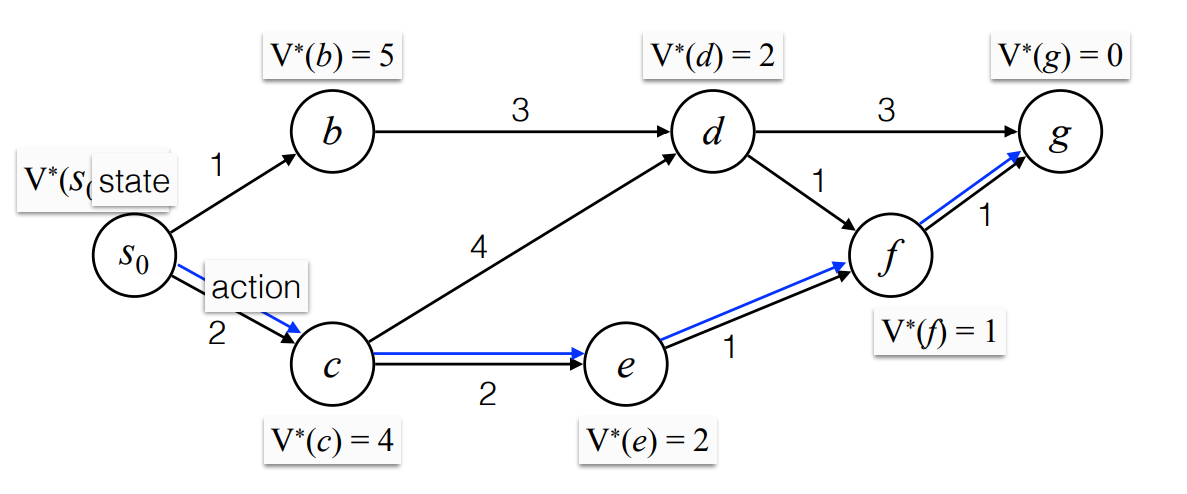
Shortest Path

• nodes: stats
• edges: actions

Greedy is not optimal.

Bellman Equation (Dynamic Programing):

$$V^\star (d) = \min\{3 + V^\star (g) ,\, 2 + V^\star (f)\$$

Stochastic Shortest Path

Markov Decision Process (MDP)

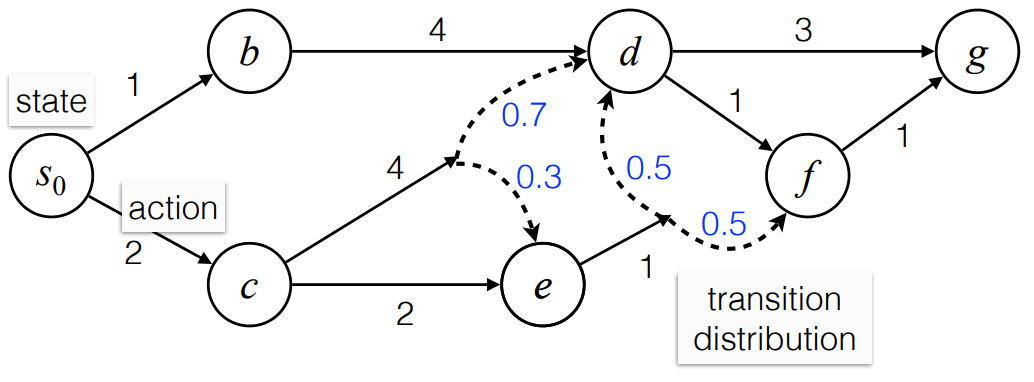
Stochastic Shortest Path

Bellman Equation

$$V^\star (c) = \min\{4 + 0.7 × V^\star (d) + 0.3 × V^\star (e) ,\, 2 + V^\star (e)\}$$

optimal policy : $\pi^\star$

Model-based RL

The states are unknown.
Learn by trial-and-error

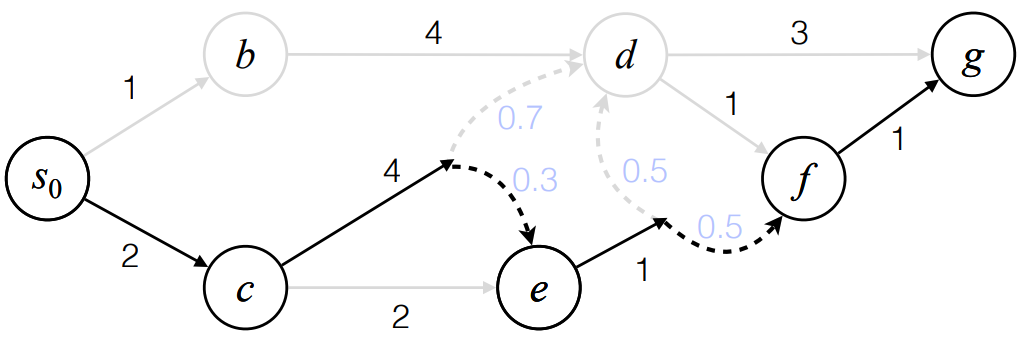
a trajectory: s0>c>e>F>G

Need to recover the graph by collecting multiple trajectories.

Use imperial frequency to find probabilities.

Assume states & actions are visited uniformly.

exploration problem

Random exploration can be inefficient:

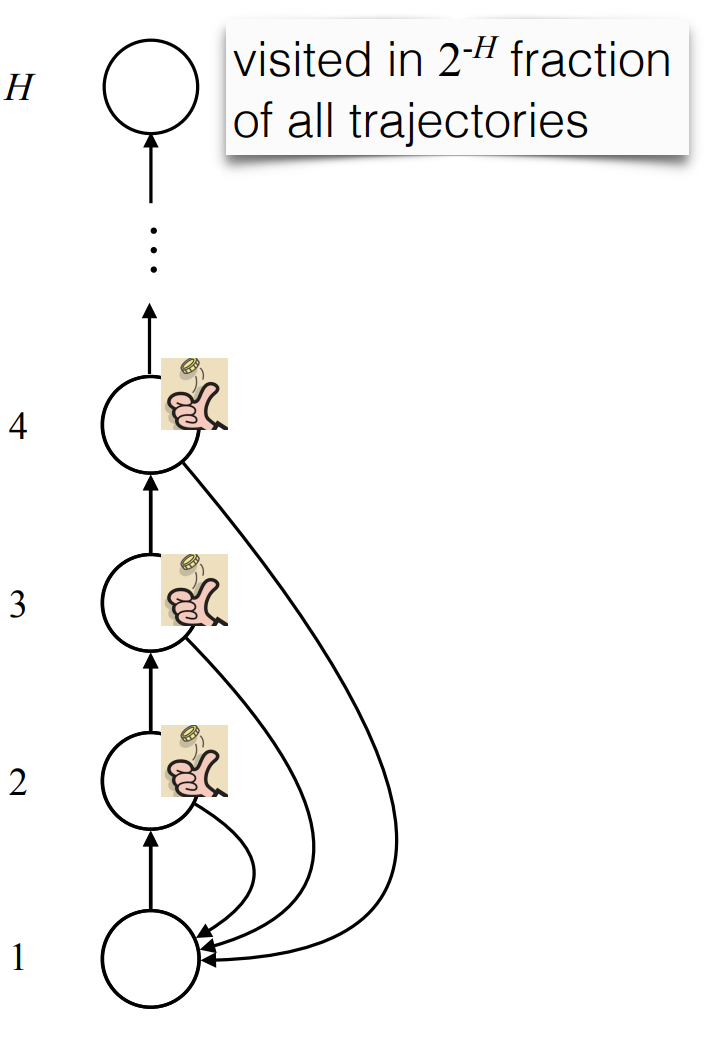
example: video game

example: video game

Objective: maximize the reward

$$\mathbb{E}\left[\sum_{t=1}^{\infty} r_t \mid \pi\right] \; \text{or} \; \mathbb{E}\left[\sum_{t=1}^{\infty} \gamma^{t-1} r_t \mid \pi\right]$$

Problem: the graph is too large

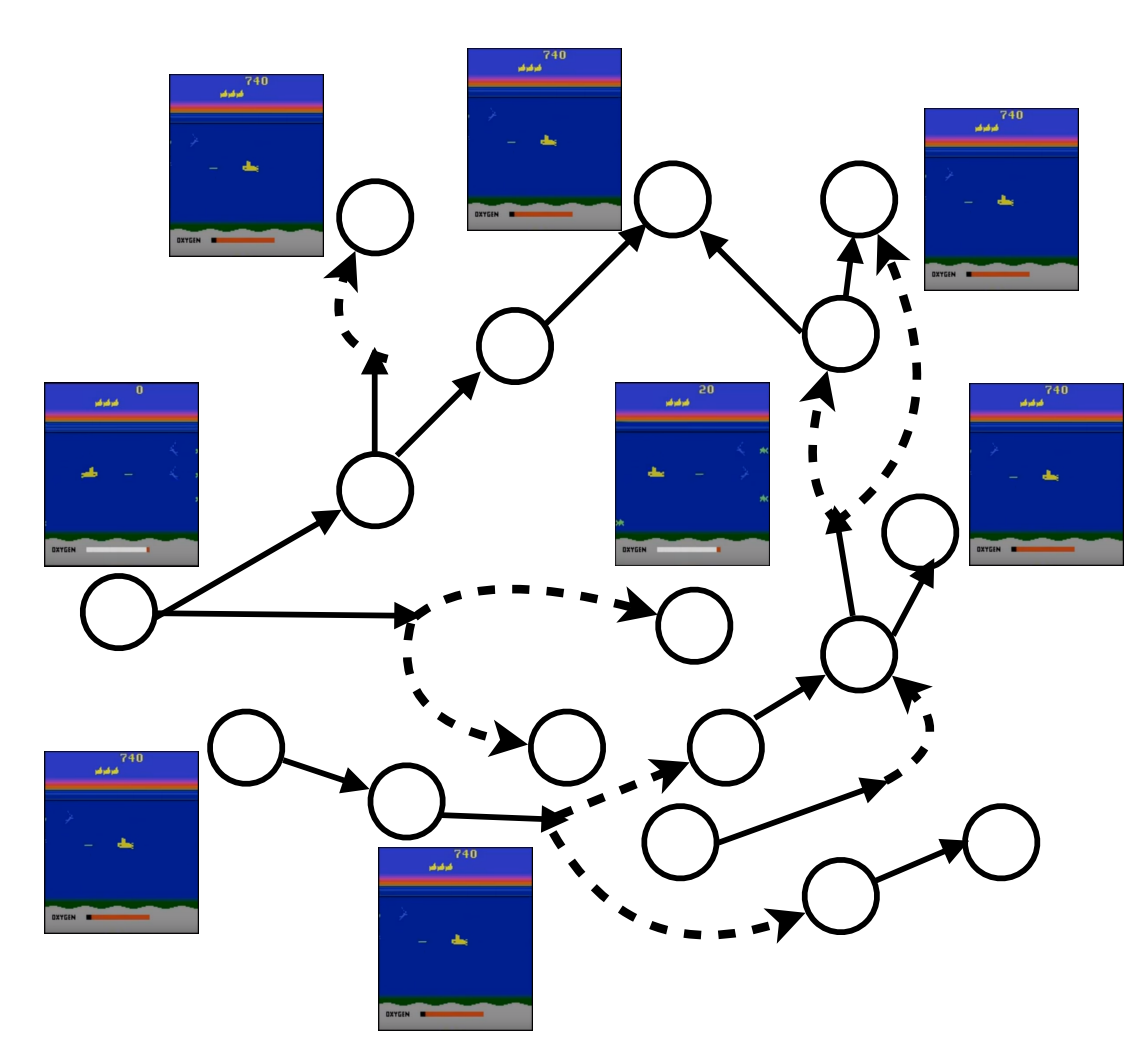
There are states that the RL model have never seen, therefore need generalization

Contextual bandits

• Even if the algorithm is good, if mamke bad actions at beginning, will not get good data.
• Keep taking bad actions (e.g. guessing wrong label on image classification), don’t know right action.
  • Compared with superivsed learning
• Multi-armed bandit

RL steps

For round t = 1, 2, …,

• For time step h=1, 2, …, H, the learner
  • Observes $x_h^{(t)}$
  • Chooses $a_h^{(t)}$
  • Receives $r_h^{(t)} \sim R(x_h^{(t)}, a_h^{(t)})$
  • Next $x_{h+1}^{(t)}$ is generated as a function of $x_h^{(t)}$ and $a_h^{(t)}$
    (or sometimes, all previous x’s and a’s within round t)