快速傅里叶变换（FFT）简介

问题引入

求多项式乘法

关于多项式

多项式除了用系数表示法外，还可以使用点值表示法。显然用 $n+1$ 个点就能表示一个 $n$ 项多项式。

表示为：

$ $f(x) = \{(x_0,y_0),(x_1,y_1), \cdots,(x_n,y_{n})\}$ $

DFT / IDFT

对系数表示的 $n$ 项多项式乘法，朴素算法需要 $O(n^2)$ 的复杂度，然而可以发现，对于同一组 $x$ 所表示的两个点值表示多项式，可以轻易地再在 $O(n)$ 时间内完成乘法计算。也就是：

f(x) = \{(x_0, f(x_0)), (x_1, f(x_1)),\cdots, (x_n, f(x_n))\}

g(x) = \{(x_0, g(x_0)), (x_1, g(x_1)),\cdots, (x_n, g(x_n))\}

f(x)g(x) = \{(x_0, f(x_0)g(x_0)), (x_1, f(x_1)g(x_1)),\cdots, (x_n, f(x_n)g(x_n))\}

而把系数表示转化为点值表示的操作叫做DFT，反过来叫IDFT。那么只需要找到高效的DFT和IDFT方法，就能得到高效的多项式乘法。

我们可以指定DFT过程中的取的不同点值 $X_i$ 为一些具有特殊性质的数，从而利用这些性质加速运算。

单位复根

复数基础

首先需要对复数有一个简单的了解。

几何意义： $z=a+bi$ 对应复平面内的点 $(a,b)$

模长： $| z| = \sqrt{a^2+b^2}$

幅角： $\theta=\arctan\frac{y}{x}$

欧拉公式： $e^{i\theta} = \cos \theta + i \sin \theta$ ，这对应着复平面上的一个单位向量。

那么 $z = | z | e^{i\theta} = r(\cos \theta + i \sin \theta)$ ，其中 $\theta$ 为 $z$ 的幅角。

进而得到，复数相乘就是模长相乘，幅角相加。

单位复根

现在考虑 $x^n = 1$ 的所有复根。首先显然有 $|x|=1$ ，那么设 $x=e^{i \theta}$ ，得到
$ $e^{i n \theta} = \cos n \theta + i \sin n \theta = 1$ $

也就是

\begin{aligned} n \theta &= 2k \pi\\ \theta &= \frac{2k\pi}{n} \; (k = 0,1,\cdots,n-1) \end{aligned}

规定其中的 $e^{\frac{2\pi}{n}}$ 为“单位根” $\omega_n$ ，那么原方程的所有复根就可以表示成

$ $x = \omega_n^k\;(k=0,1,\cdots,n-1)$ $

现在考察其几何意义，不难发现这些根所表示的点就是绕单位圆一周 $n$ 等分的点。

比如三次的情形：

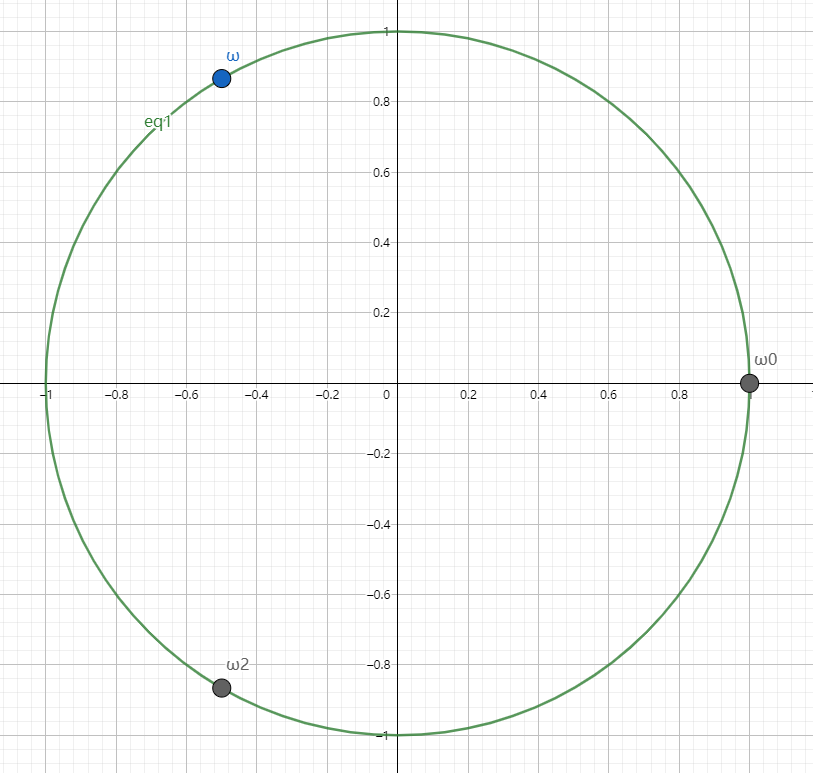
三次单位根

一些重要的性质：

\begin{aligned} \omega_n^n&=1\\ \omega_n^k&=\omega_{2n}^{2k}\\ \omega_{2n}^{k+n}&=-\omega_{2n}^k\\ \end{aligned}

结合一下几何意义，这些结论是比较显然的。

而在DFT的过程中，带入的 $\{ x_i \}$ 正是 $\{ \omega_n^0, \omega_n^1,\cdots ,\omega_n^n-1 \}$

分治

知道了带代入哪些值，求解的过程就需要合理地利用这些值的性质。

考虑分治，将多项式分为奇次项和偶次项处理。

举个例子，对于一共 $8$ 项的多项式

f(x) = a_0 + a_1x + a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+a_7x^7

按照次数的奇偶来分成两组，然后右边提出来一个 $x$

\begin{aligned} f(x) &= (a_0+a_2x^2+a_4x^4+a_6x^6) + (a_1x+a_3x^3+a_5x^5+a_7x^7)\\ &= (a_0+a_2x^2+a_4x^4+a_6x^6) + x(a_1+a_3x^2+a_5x^4+a_7x^6) \end{aligned}

分别用奇偶次次项数建立新的函数

\begin{aligned} G(x) &= a_0+a_2x+a_4x^2+a_6x^3\\ H(x) &= a_1+a_3x+a_5x^2+a_7x^3 \end{aligned}

那么原来的 $f(x)$ 用新函数表示为

f(x)=G\left(x^2\right) + x \times H\left(x^2\right)

利用单位复根的性质得到

\begin{aligned} f(\omega_n^k) &=G((\omega_n^k)^2) + \omega_n^k \times H((\omega_n^k)^2)\\ &=G(\omega_n^{2k}) + \omega_n^k \times H(\omega_n^{2k})\\ &=G(\omega_{n/2}^k) + \omega_n^k \times H(\omega_{n/2}^k) \end{aligned}

同理可得

\begin{aligned} f(\omega_n^{k+n/2}) &=G(\omega_n^{2k+n}) + \omega_n^{k+n/2} \times H(\omega_n^{2k+n})\\ &=G(\omega_n^{2k}) - \omega_n^k \times H(\omega_n^{2k})\\ &=G(\omega_{n/2}^k) - \omega_n^k \times H(\omega_{n/2}^k) \end{aligned}

由此我们发现

$ $\{H(\omega_{n/2}^0), \cdots , H(\omega_{n/2}^{n/2-1}) \} \; \{G(\omega_{n/2}^0), \cdots , G(\omega_{n/2}^{n/2-1}) \}$ $

这两个子问题的形式与原问题

$ $\{H(\omega_n^0), \cdots , H(\omega_n^{n-1}) \}$ $

是完全相同的，而且两个子问题的答案能在 $O(n)$ 时间内合并得到原问题的答案。于是总时间复杂度为 $O(n \log n)$ （参考归并排序）这就是DFT操作。

另外需要注意将 $f$ 的高次补 $0$ 以满足长度 $n$ 是 $2$ 的整数次幂。

参考代码

IDFT

现在我们已经用 $O(n \log n)$ 的时间得到了两个多项式的点值形式，从而通过点值相乘得到了答案多项式的点值形式。还剩下通过IDFT将答案多项式的点值形式转化为系数形式。要如何操作？

其实只需要简单地把单位复根 $\omega_n = e^{\frac{2\pi}{n}}$ 变为其倒数 $\frac{1}{\omega_n^k} = e^{ - \frac{2\pi}{n}}$ ，再进行一遍DFT就可以了（即：将有第一遍DFT得到的点值看作“系数”，在此基础上带入 $\frac{1}{\omega_n^k} \; (k = 0,1,\cdots, n - 1)$ 求值）。

下面证明：

原多项式：

$ $f(x) = \sum_{i=0}^{n-1} a_i x^i$ $

得到的点值：

$ $y_i = f(\omega_n^i) = \sum_{j=0}^{n-1} a_j \omega_n^{ij}$ $

将点值 $y_i$ 作为系数得到的新多项式：

$ $g(x) = \sum_{i=0}^{n-1}y_i x^i$ $

在新多项式里代入：

\begin{aligned} g(\omega_n^{-k}) &= \sum_{i=0}^{n-1}y_i \omega_n^{-ik} \\ &= \sum_{i=0}^{n-1}\sum_{j=0}^{n-1} a_j \omega_n^{ij} \omega_n^{-ik} \\ &= \sum_{j=0}^{n-1} a_j \sum_{i=0}^{n-1} (\omega_n^{j-k})^i \\ \end{aligned}

记 $S\left(\omega_n^a\right)=\sum_{i=0}^{n-1}\left(\omega_n^a\right)^i$ 。

当 $a=0 \pmod{n}$ 时， $S\left(\omega_n^a\right)=n$ 。

当 $a\neq 0 \pmod{n}$ 时，我们错位相减

\begin{aligned} S\left(\omega_n^a\right)&=\sum_{i=0}^{n-1}\left(\omega_n^a\right)^i\\ \omega_n^a S\left(\omega_n^a\right)&=\sum_{i=1}^{n}\left(\omega_n^a\right)^i\\ S\left(\omega_n^a\right)&=\frac{\left(\omega_n^a\right)^n-\left(\omega_n^a\right)^0}{\omega_n^a-1}=0\\ \end{aligned}

也就是说

S\left(\omega_n^a\right)= \left\{\begin{aligned} n,a=0\\ 0,a\neq 0 \end{aligned}\right.

那么代回原式

g(\omega_n^{-k}) = \sum_{j=0}^{n-1}a_jS\left(\omega_n^{j-k}\right)=a_k\cdot n

所以只需要写一个函数，传入参数 $\texttt{op}$ ， $\texttt{op == 1}$ 时为DFT， $\texttt{op == -1}$ 为IDFT，进行IDFT时再将各个结果 $\texttt{/n}$ 即可。

另有方法二，原理基本相同

非递归

为了提高运行效率，可以将FFT改成非递归的写法。

每次递归实际上就是将奇数位置和偶数位置的系数分别放在头尾。

\begin{aligned} &\{x_0, x_1, x_2, x_3, x_4, x_5, x_6, x_7\} \\ &\{x_0, x_2, x_4, x_6\},\{x_1, x_3, x_5, x_7 \} \\ &\{x_0,x_4\} \{x_2, x_6\},\{x_1, x_5\},\{x_3, x_7 \} \\ &\{x_0\}\{x_4\}\{x_2\}\{x_6\}\{x_1\}\{x_5\}\{x_3\}\{x_7 \} \end{aligned}

通过手动模拟可以发现，这样的操作实际上就是对所有数以最后一个二进制位为第一关键字、倒数第二个二进制位为第二关键字……进行的排序，即按照二进制对称翻转后的数进行排序。我们称这个变换为位逆序置换（蝴蝶变换）。

记 $R(x)$ 为 $x$ 位逆序置换后的结果。

显然朴素算法能再 $O(n \log n)$ 的时间内求解 $R(x)$ ，现在考虑递推优化。

可以发现 $R(x)$ 与 $R(x/2)$ 只有一个二进制位的差别，于是简单地模拟一下就可以写出 $k$ 个二进制位时的递推式：

R(x)=\left\lfloor \frac{R\left(\left\lfloor \frac{x}{2} \right\rfloor\right)}{2} \right\rfloor + (x\bmod 2)\times \frac{len}{2}

其中 $len = 2^k$ 。

进行为逆序置换的代码：

void change(Complex y[], int n) {
    rep(i, 0, n - 1) {
        rev[i] = rev[i >> 1] >> 1;
        if (i & 1) rev[i] |= n >> 1;
    }
    rep(i, 0, n - 1) if (i < rev[i]) swap(y[i], y[rev[i]]);
}

（其中的 $\texttt{if (i < rev[i])}$ ）是为了防止重复交换）

示例代码

模板：高精度乘法

#include <bits/stdc++.h>
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define per(i, a, b) for (int i = (a); i >= (b); i--)
#define D(x) cout << #x << " : " << x << endl
using namespace std;
const int N = 1 << 21;

struct Complex {
    double x, y;
    Complex(double _x = 0.0, double _y = 0.0) {
        x = _x;
        y = _y;
    }
    friend Complex operator+(Complex a, Complex b) {
        return Complex(a.x + b.x, a.y + b.y);
    }
    friend Complex operator-(Complex a, Complex b) {
        return Complex(a.x - b.x, a.y - b.y);
    }
    friend Complex operator*(Complex a, Complex b) {
        return Complex(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x);
    }
};
int rev[N];

/* 位逆序置换 */
void change(Complex y[], int n) {
    rep(i, 0, n - 1) {
        rev[i] = rev[i >> 1] >> 1;
        if (i & 1) rev[i] |= n >> 1;
    }
    rep(i, 0, n - 1) if (i < rev[i]) swap(y[i], y[rev[i]]);
}

void fft(Complex y[], int n, int op) {
    /* op == 1: DFT
       op == -1: IDFT */
    change(y, n);
    for (int h = 2; h <= n; h *= 2) {
        Complex wn(cos(2 * M_PI / h), sin(op * 2 * M_PI / h));
        for (int j = 0; j < n; j += h) {
            Complex w(1, 0);
            rep(k, j, j + h / 2 - 1) {
                Complex u = y[k], t = w * y[k + h / 2];
                y[k] = u + t, y[k + h / 2] = u - t;
                w = w * wn;
            }
        }
    }
    if (op == -1) rep(i, 0, n - 1) y[i].x /= n;
}

char a[N], b[N];
Complex x[N], y[N];
int ans[N];

int main() {
    scanf("%s %s", a, b);
    int l1 = strlen(a), l2 = strlen(b), n = 1;
    while (n < l1 + l2) n *= 2;
    rep(i, 0, l1 - 1) x[i] = Complex(a[l1 - 1 - i] - '0', 0);
    rep(i, l1, n - 1) x[i] = Complex(0, 0);
    rep(i, 0, l2 - 1) y[i] = Complex(b[l2 - 1 - i] - '0', 0);
    rep(i, l2, n - 1) y[i] = Complex(0, 0);
    fft(x, n, 1), fft(y, n, 1);
    rep(i, 0, n - 1) x[i] = x[i] * y[i];
    fft(x, n, -1);
    rep(i, 0, n - 1) ans[i] = int(x[i].x + 0.5);
    rep(i, 0, n - 1) ans[i + 1] += ans[i] / 10, ans[i] %= 10;
    while (ans[n - 1] == 0 && n > 1) n--;
    per(i, n - 1, 0) putchar(ans[i] + '0');
    return 0;
}

参考

https://oi-wiki.org/math/poly/fft/

数学

#FFT #多项式

快速傅里叶变换（FFT）简介

https://yzzzf.xyz/2021/09/07/fft/

Author

Zifan Ying

Posted on

September 7, 2021

Licensed under

快速数论变换（NTT） Previous

树状数组进阶应用 Next