一些凸包有关的算法
判断点在凸包内
主要介绍二分法^l1
二分法
如图,
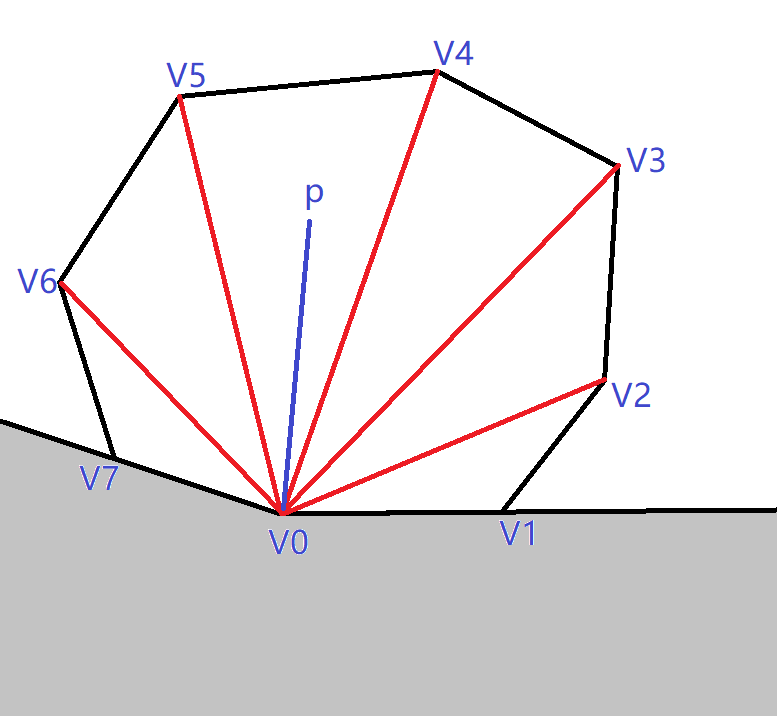
可以通过向量叉积得到任意 和 的左右关系。
先通过 和 排除 在灰色区域的情况。
显然通过二分,就能找到 使得 在 和 之间
接下来只需要判断 是否在 左侧即可(假定凸包以逆时针方向给出)。
Code
#include <bits/stdc++.h>
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define per(i, a, b) for (int i = (a); i >= (b); i--)
#define D(x) cout << #x << " : " << x << endl
using namespace std;
const int N = 1001;
struct point {
int x, y;
point() { x = y = 0; }
point(int p, int q) { x = p, y = q; }
friend point operator-(point p, point q) { return point(p.x - q.x, p.y - q.y); }
friend int operator*(point p, point q) { return p.x * q.y - p.y * q.x; } // cross product
} v[N];
int n;
bool check(point p) {
if ((v[1] - v[0]) * (p - v[0]) < 0) return false;
if ((v[n - 1] - v[0]) * (p - v[0]) > 0) return false;
int l = 1, r = n - 1, mid;
while (l <= r) {
mid = (l + r) / 2;
if ((v[mid] - v[0]) * (p - v[0]) > 0)
l = mid + 1;
else
r = mid - 1;
}
return (v[l] - v[r]) * (p - v[r]) > 0;
}
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n;
rep(i, 0, n - 1) cin >> v[i].x >> v[i].y;
for (;;) {
point q;
cin >> q.x >> q.y;
cout << (check(q) ? "In" : "Out") << endl;
}
return 0;
}其他方法
判断内角和 ,射线相交……
凸包极值点
即一个凸包在某一个向量 方向上投影的极值点。^l2
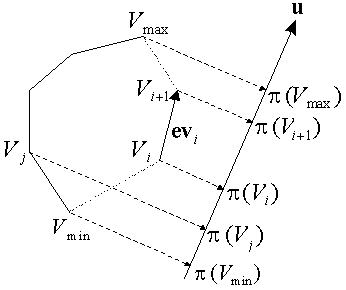
对于任意向量 ,可以通过 的正负性判断 在 投影的方向。
二分法
分类讨论:
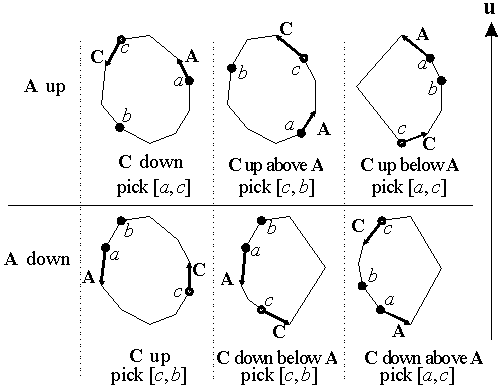
Code
#include <bits/stdc++.h>
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define per(i, a, b) for (int i = (a); i >= (b); i--)
#define D(x) cout << #x << " : " << x << endl
using namespace std;
const int N = 1001;
struct point {
int x, y;
point() { x = y = 0; }
point(int p, int q) { x = p, y = q; }
friend point operator-(point p, point q) { return point(p.x - q.x, p.y - q.y); }
friend int operator*(point p, point q) { return p.x * q.x + p.y * q.y; } // dot product
} v[N], u;
int n;
inline bool up(int i, int j) { return (v[j] - v[i]) * u > 0; } // check vector i -> j
inline bool up(int i) { return up(i, i == n - 1 ? 0 : i + 1); }
int find_max() {
if (!up(0) && up(n - 1)) return 0;
int l = 0, r = n, mid;
while (l < r) {
mid = (l + r) / 2;
if (!up(mid) && up(mid - 1)) return mid;
if (up(l)) {
if (!up(mid))
r = mid;
else {
if (up(l, mid))
l = mid;
else
r = mid;
}
}
else {
if (up(mid))
l = mid;
else {
if (!up(l, mid))
l = mid;
else
r = mid;
}
}
}
}
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
cin >> n;
rep(i, 0, n - 1) cin >> v[i].x >> v[i].y;
cin >> u.x >> u.y;
cout << find_max() << endl;
return 0;
}注意 初值为 。
点到凸包的切线
容易发现,点到凸包的切线实际上就是凸包上各个点到某个点极角的极值,只要能得到两个点 和 关于点 的“上下关系”,那么就可以套用凸包极值点的二分策略。
显然只要用 的正负性判断就行了。
Code
在凸包极值点代码的基础上修改:
改成叉积:
friend int operator*(point p, point q) { return p.x * q.y - p.y * q.x; } // cross product改变判定方式:
inline bool up(int i, int j) { return (v[j] - u) * (v[i] - u) > 0; } // check vector i -> j一些凸包有关的算法
https://yzzzf.xyz/2021/08/24/convexhull_algo/